O que o aluno poderá aprender com esta aula
• Identificar os diversos tipos de poliedros
• Identificar quantidades de faces, vértices e arestas de um polígono
• Identificar quantidades de faces, vértices e arestas de um polígono
Duração das atividades
4 aulas de 50 minutos cada
Conhecimentos prévios trabalhados pelo professor com o aluno
• Conceito de côncavo e convexo
Estratégias e recursos da aula
No laboratório de informática (2 aulas)
Olá Professor, vamos apresentar uma maneira divertida de trabalhar o assunto “Poliedros” com nossos alunos. Para iniciar o assunto, apresente a eles algumas charadas para eles tentem descobrir as respostas:
• Sou o poliedro regular mais conhecido, nos cassinos do mundo todo sou muito utilizado. Possuo 8 vértices, 12 arestas e minhas faces são quadrangulares. Quem sou eu? (Hexaedro);
• Fui um poliedro regular muito utilizado por povos da antiguidade a mais de dois mil anos e por isso sou conhecido até hoje. Possuo 4 vértices, 6 arestas e faces triangulares... Quem sou eu? (Tetraedro);
• Sou um poliedro regular, mas não sou muito conhecido. Possuo 6 vértices, 12 arestas e minhas faces são triangulares. Para saber o número de faces que possuo multiplique o quarto número natural por dois... Quem sou eu? (Octaedro);
• Sou um poliedro regular muito difícil de ser feito, porém muito bonito. Sou o que possuo o maior número de faces além de 12 vértices e 30 arestas... Quem sou eu? (Icosaedro).
Peça aos seus alunos que acessem o sítio http://www.di.falm.edu.br/projetos/infoeduc/OAPoliedros.swf. Trata-se de um aplicativo, on-line e autoinstrutivo, que trabalha toda a parte teórica bem como os exercícios on-line. Oriente aos alunos para que executem os comandos que apareceram na parte inferior da tela.

Professor, no sítio http://www2.ucg.br/design/da2/solidosgeometricos.pdf existe um material, em pdf, com o resumo do assunto “Sólidos geométricos” e suas planificações. Pode ser útil para tirar as dúvidas que os alunos ainda tenham sobre o assunto. Aproveite o momento também para dedicar um tempo para que eles possam montar as planificações, ficando mais fácil o entendimento da Relação de Euler.
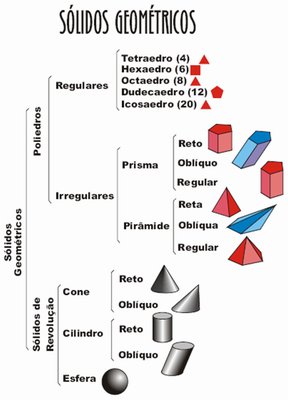
Professor converse um pouco com seus alunos sobre a vida de Euler, http://pt.wikipedia.org/wiki/Leonhard_Euler, mostre o quanto ele produziu em vida e em seguida apresente a eles a “Relação de Euler”, para isto acesse o sítio http://www.somatematica.com.br/emedio/espacial/espacial9.php. Existem outros links disponíveis em:
• http://mathematikos.psico.ufrgs.br/disciplinas/ufrgs/mat010392k2/ens22k2/sinteticos/pagina4.html
• http://www.slideshare.net/jsaltmann/trabalho-mec-slaides-presentation
• http://www.klickeducacao.com.br/2006/materia/20/display/0,5912,POR-20-94-953-,00.html
• http://www.educacao.te.pt/jovem/index.jsp?p=117&idArtigo=369
• http://www.atractor.pt/simetria/matematica/docs/ainda_reg2.html
Professor, elabore uma lista de exercícios para que seus alunos possam praticar um pouco. Existem alguns modelos disponíveis em:
• http://www.daescola.com.br/uploads/zaccaria.g12.br/exercicios/poliedros_2009.pdf
• http://prevestibularonline.blogspot.com/2008/08/exercicios-poliedro.html
• http://www.peretz.com.br/professores/sejadmais05/exercicios/200405/exe-mat-2s-07.pdf
• http://www.anglocampinas.com.br:8080/script/site_anglo2004/aluno_anglo/salas_materias/matematica/2008/arquivos/Exerc%C3%ADcios%20poliedros.doc
• http://www.slideshare.net/jsaltmann/trabalho-mec-slaides-presentation
Na sala de aula ( 2 aulas)
Para fixar o conteúdo utilizaremos uma atividade lúdica, o jogo “Cara a cara dos poliedros”. Os objetivos deste jogo são o desenvolvimento do raciocínio lógico-dedutivo e a identificação de poliedros pelos seus nomes, relacionando-os a algumas propriedades geométricas que envolvem faces, vértices e arestas.
Organização da classe: em duplas ou duas duplas que jogam um contra a outra.
Recursos necessários:
• dois baralhos com nomes de poliedros ( 20 cartas em cada baralho) em duas cores distintas;

• um baralho de propriedades (26 cartas);

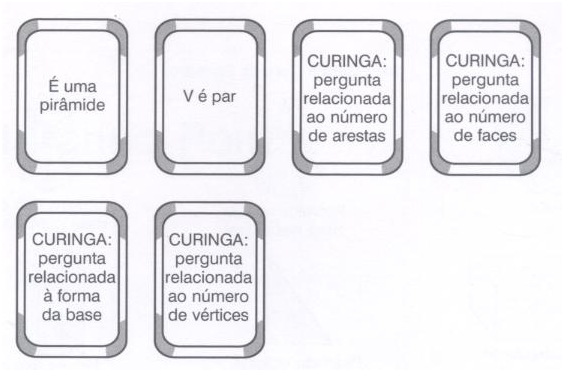
• cartazete com os sólidos e seus nomes, papel e lápis.

Regras:
1. Cada jogador recebe um conjunto de cartas com nomes de poliedros que ficam sobre a mesa voltadas para cima à frente de cada jogador, e as cartas propriedades são embaralhadas e colocadas no centro da mesa voltadas para baixo.
2. O cartazete é colocado de modo que os jogadores possam vê-lo durante o jogo.
3. Os jogadores escolhem um poliedro do cartazete, sem que seu oponente saiba qual é, e registram o nome do poliedro escolhido.
4. O objetivo de cada jogador é descobrir o poliedro de seu oponente.
5. Decide-se quem começa e, a partir daí, os participantes ou as duplas jogam alternadamente.
6. Na sua vez, o jogador retira uma carta do baralho de propriedades e pergunta a seu oponente se o poliedro escolhido por ele tem aquela propriedade. O oponente deve responder apenas sim ou não. O jogador deverá excluir os poliedros que não lhe interessam. Por exemplo, se a carta retirada contiver “Algumas faces” e a resposta for sim, ficam excluídos todos os poliedros que não contêm nenhuma face triangular; porém, se a resposta for não, significa que o poliedro escondido não tem faces triangulares, o que exclui todas as pirâmides, o octaedro e os primas de base triangular.
7. O outro jogador procede do mesmo modo.
8. Ganha o jogo que acertar o nome do poliedro escolhido por seu oponente.
Algumas explorações possíveis:
Após jogar algumas vezes, é possível solicitar a resolução de situações como:
• Se a carta de propriedades sorteada for “Algumas faces são congruentes” e a resposta for sim, quais poliedros podem ser excluídos?
• Quais cartas de poliedros são eliminadas quando a resposta é sim para a carta de propriedades “F é ímpar?”.
• Se, em uma sequência de duas jogadas, você souber que o sólido de seu oponente tem as propriedades “Possui apenas um par de faces paralelas e F é ímpar”, quais poliedros ainda ficariam na mesa? Há alguma propriedade enunciada que permita a você se decidir por um único poliedro?
• Escolha uma carta com o nome de um poliedro. Dentre as cartas propriedades, selecione aquelas que são satisfeitas pelo poliedro escolhido.
Comunicando a aprendizagem
Algumas possibilidades de os alunos comunicarem o que aprenderam durante o jogo são:
1. Selecionar duas cartas de poliedros e listar as propriedades pertinentes a cada uma.
2. Propor que os alunos selecionem quatro cartas propriedades de tal modo que, do conjunto de cartas com nomes de poliedros, possam fazer exclusões que lhes permitam ficar apenas com a carta de poliedro “Prisma oblíquo de base quadrada”.
Variações
A am pliação desse jogo pode ser feita inserindo-se novas cartas de poliedros, cartas de propriedades e outros sólidos geométricos, como, por exemplo, o cilindro, o cone e a esfera.
Outra possibilidade é jogar sem as cartas propriedades. Nessa versão o jogador formularia as perguntas.
Fonte: Caderno do Mathema, Jogos de matemática de 1º a 3º ano, Ensino Médio. Editora Artmed.
Olá Professor, vamos apresentar uma maneira divertida de trabalhar o assunto “Poliedros” com nossos alunos. Para iniciar o assunto, apresente a eles algumas charadas para eles tentem descobrir as respostas:
• Sou o poliedro regular mais conhecido, nos cassinos do mundo todo sou muito utilizado. Possuo 8 vértices, 12 arestas e minhas faces são quadrangulares. Quem sou eu? (Hexaedro);
• Fui um poliedro regular muito utilizado por povos da antiguidade a mais de dois mil anos e por isso sou conhecido até hoje. Possuo 4 vértices, 6 arestas e faces triangulares... Quem sou eu? (Tetraedro);
• Sou um poliedro regular, mas não sou muito conhecido. Possuo 6 vértices, 12 arestas e minhas faces são triangulares. Para saber o número de faces que possuo multiplique o quarto número natural por dois... Quem sou eu? (Octaedro);
• Sou um poliedro regular muito difícil de ser feito, porém muito bonito. Sou o que possuo o maior número de faces além de 12 vértices e 30 arestas... Quem sou eu? (Icosaedro).
Peça aos seus alunos que acessem o sítio http://www.di.falm.edu.br/projetos/infoeduc/OAPoliedros.swf. Trata-se de um aplicativo, on-line e autoinstrutivo, que trabalha toda a parte teórica bem como os exercícios on-line. Oriente aos alunos para que executem os comandos que apareceram na parte inferior da tela.

Professor, no sítio http://www2.ucg.br/design/da2/solidosgeometricos.pdf existe um material, em pdf, com o resumo do assunto “Sólidos geométricos” e suas planificações. Pode ser útil para tirar as dúvidas que os alunos ainda tenham sobre o assunto. Aproveite o momento também para dedicar um tempo para que eles possam montar as planificações, ficando mais fácil o entendimento da Relação de Euler.

Professor converse um pouco com seus alunos sobre a vida de Euler, http://pt.wikipedia.org/wiki/Leonhard_Euler, mostre o quanto ele produziu em vida e em seguida apresente a eles a “Relação de Euler”, para isto acesse o sítio http://www.somatematica.com.br/emedio/espacial/espacial9.php. Existem outros links disponíveis em:
• http://mathematikos.psico.ufrgs.br/disciplinas/ufrgs/mat010392k2/ens22k2/sinteticos/pagina4.html
• http://www.slideshare.net/jsaltmann/trabalho-mec-slaides-presentation
• http://www.klickeducacao.com.br/2006/materia/20/display/0,5912,POR-20-94-953-,00.html
• http://www.educacao.te.pt/jovem/index.jsp?p=117&idArtigo=369
• http://www.atractor.pt/simetria/matematica/docs/ainda_reg2.html
Professor, elabore uma lista de exercícios para que seus alunos possam praticar um pouco. Existem alguns modelos disponíveis em:
• http://www.daescola.com.br/uploads/zaccaria.g12.br/exercicios/poliedros_2009.pdf
• http://prevestibularonline.blogspot.com/2008/08/exercicios-poliedro.html
• http://www.peretz.com.br/professores/sejadmais05/exercicios/200405/exe-mat-2s-07.pdf
• http://www.anglocampinas.com.br:8080/script/site_anglo2004/aluno_anglo/salas_materias/matematica/2008/arquivos/Exerc%C3%ADcios%20poliedros.doc
• http://www.slideshare.net/jsaltmann/trabalho-mec-slaides-presentation
Na sala de aula ( 2 aulas)
Para fixar o conteúdo utilizaremos uma atividade lúdica, o jogo “Cara a cara dos poliedros”. Os objetivos deste jogo são o desenvolvimento do raciocínio lógico-dedutivo e a identificação de poliedros pelos seus nomes, relacionando-os a algumas propriedades geométricas que envolvem faces, vértices e arestas.
Organização da classe: em duplas ou duas duplas que jogam um contra a outra.
Recursos necessários:
• dois baralhos com nomes de poliedros ( 20 cartas em cada baralho) em duas cores distintas;

• um baralho de propriedades (26 cartas);


• cartazete com os sólidos e seus nomes, papel e lápis.

Regras:
1. Cada jogador recebe um conjunto de cartas com nomes de poliedros que ficam sobre a mesa voltadas para cima à frente de cada jogador, e as cartas propriedades são embaralhadas e colocadas no centro da mesa voltadas para baixo.
2. O cartazete é colocado de modo que os jogadores possam vê-lo durante o jogo.
3. Os jogadores escolhem um poliedro do cartazete, sem que seu oponente saiba qual é, e registram o nome do poliedro escolhido.
4. O objetivo de cada jogador é descobrir o poliedro de seu oponente.
5. Decide-se quem começa e, a partir daí, os participantes ou as duplas jogam alternadamente.
6. Na sua vez, o jogador retira uma carta do baralho de propriedades e pergunta a seu oponente se o poliedro escolhido por ele tem aquela propriedade. O oponente deve responder apenas sim ou não. O jogador deverá excluir os poliedros que não lhe interessam. Por exemplo, se a carta retirada contiver “Algumas faces” e a resposta for sim, ficam excluídos todos os poliedros que não contêm nenhuma face triangular; porém, se a resposta for não, significa que o poliedro escondido não tem faces triangulares, o que exclui todas as pirâmides, o octaedro e os primas de base triangular.
7. O outro jogador procede do mesmo modo.
8. Ganha o jogo que acertar o nome do poliedro escolhido por seu oponente.
Algumas explorações possíveis:
Após jogar algumas vezes, é possível solicitar a resolução de situações como:
• Se a carta de propriedades sorteada for “Algumas faces são congruentes” e a resposta for sim, quais poliedros podem ser excluídos?
• Quais cartas de poliedros são eliminadas quando a resposta é sim para a carta de propriedades “F é ímpar?”.
• Se, em uma sequência de duas jogadas, você souber que o sólido de seu oponente tem as propriedades “Possui apenas um par de faces paralelas e F é ímpar”, quais poliedros ainda ficariam na mesa? Há alguma propriedade enunciada que permita a você se decidir por um único poliedro?
• Escolha uma carta com o nome de um poliedro. Dentre as cartas propriedades, selecione aquelas que são satisfeitas pelo poliedro escolhido.
Comunicando a aprendizagem
Algumas possibilidades de os alunos comunicarem o que aprenderam durante o jogo são:
1. Selecionar duas cartas de poliedros e listar as propriedades pertinentes a cada uma.
2. Propor que os alunos selecionem quatro cartas propriedades de tal modo que, do conjunto de cartas com nomes de poliedros, possam fazer exclusões que lhes permitam ficar apenas com a carta de poliedro “Prisma oblíquo de base quadrada”.
Variações
A am pliação desse jogo pode ser feita inserindo-se novas cartas de poliedros, cartas de propriedades e outros sólidos geométricos, como, por exemplo, o cilindro, o cone e a esfera.
Outra possibilidade é jogar sem as cartas propriedades. Nessa versão o jogador formularia as perguntas.
Fonte: Caderno do Mathema, Jogos de matemática de 1º a 3º ano, Ensino Médio. Editora Artmed.
Recursos Complementares
Avaliação
A avaliação poderá ocorrer durante as atividades desenvolvidas na aula. Observe:
• A participação dos alunos nas discussões, na atividade de consolidação dos conhecimentos e na atividade lúdica;
• Construção de poliedros e apresentação dos trabalhos em grupo;
• Participação e Blogs. Os alunos podem criar um ou participar de algum já criado, como sugestão temos http://br.answers.yahoo.com/question/index?qid=20090603154024AA0yg5l.
• A participação dos alunos nas discussões, na atividade de consolidação dos conhecimentos e na atividade lúdica;
• Construção de poliedros e apresentação dos trabalhos em grupo;
• Participação e Blogs. Os alunos podem criar um ou participar de algum já criado, como sugestão temos http://br.answers.yahoo.com/question/index?qid=20090603154024AA0yg5l.
Sem comentários:
Enviar um comentário