O cone é um importante sólido da geometria. Estão relacionados ao cone, elementos importantes da matemática como as cônicas que envolvem as curvas da parábola, círculo, elipse e hipérbole. Assim, um bom entendimento do cone pode também auxiliar os alunos em outros conhecimentos importantes relacionados com a geometria. Nessa aula também apresentamos uma forma de manipular o sólido em 3D usando o programa de apresentações do BrOffice, o Impress (http://www.broffice.org).
Abaixo uma imagem de um cone que o professor pode apresentar aos alunos.
Recurso disponível em:
ConeSugerimos que o professor proponha que os alunos conheçam melhor o cone por meio da criação dos seus próprios cones. Para isso o Impress oferece um excelente recurso de desenho de objetos em 3D. Vamos ver como isso pode ser feito.
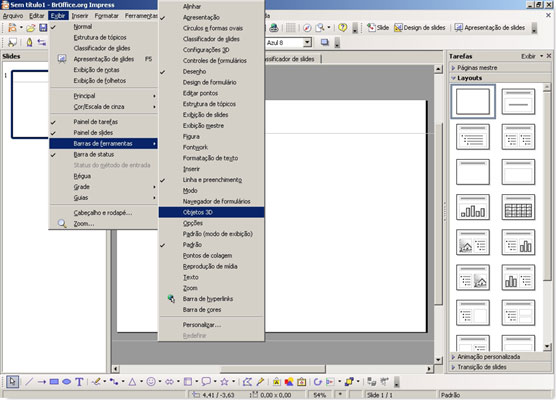
O primeiro passo é exibir a barra de ferramentas de desenho para objetos em 3D.
Basta seguir o caminho indicado na figura acima: Exibir > Barra de ferramentas > Objetos 3D
Clicando no ícone do cone pode-se desenhar, girar, redimensionar e alterar a cor do cone em 3 dimensões.
Observe o exemplo abaixo:
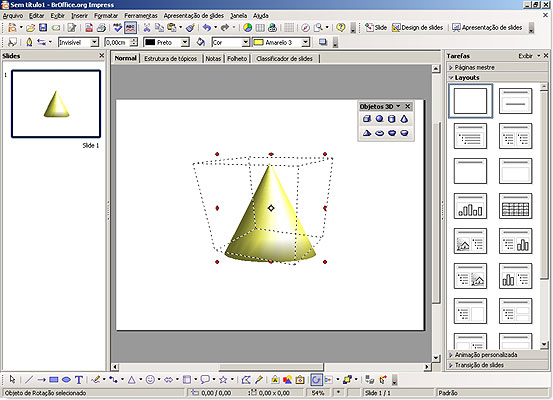
Uma vez que os alunos tenham tido a oportunidade de manipular e conhecer um pouco mais sobre o cone, pode-se partir para um aprofundamento do estudo do cone. A classificação de um cone é o próximo passo.
Classificação de um cone circular
Existem dois tipos de cones a serem apresentados aos alunos.
1. O Cone Reto
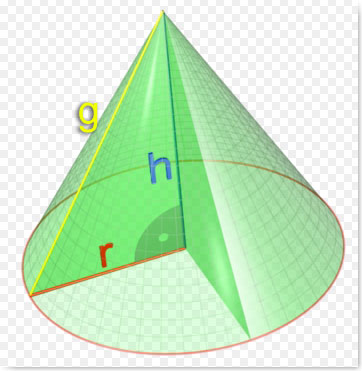
Fonte: http://en.wikipedia.org/wiki/Image:Cone_3d.png (modificada pelo autor)
O cone reto é o cone cujo eixo de rotação é perpendicular à base. Porém, antes de apresentar a definição, é importante que o professor pergunte aos alunos que características eles observam no cone e se eles conseguem identificar o motivo da nomenclatura do cone.
2. O Cone Oblíquo
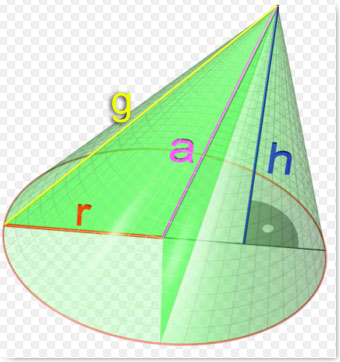
Fonte: http://en.wikipedia.org/wiki/Image:Cone_3d.png (modificada pelo autor)
No caso deste cone, é fácil constatar que ele é chamado de oblíquo em função da inclinação do eixo de rotação em relação à base.
Elementos de um cone circular
Possivelmente os alunos identifiquem rapidamente o raio e a altura dos cones apresentados. A idenficação dos elementos são importantes para que possam ser realizados cálculos quando necessários. Observando as imagens podemos considerar a existência dos seguintes elementos:
* altura: a distância h
* geratriz: segmento g entre as extremidades, da ponta à base.
* eixo: representado por a no cone oblíquo. No caso do cone reto, o eixo coincide com a linha da altura.
* raio: identificado por r.
Área e Volume de um Cone
Área
Utilizaremos a planificação de um cone circular reto para tornar o cálculo mais compreensível. Basicamente, o cálculo a ser feito é a da soma das áreas da planificação do cone somada à área da base do cone.
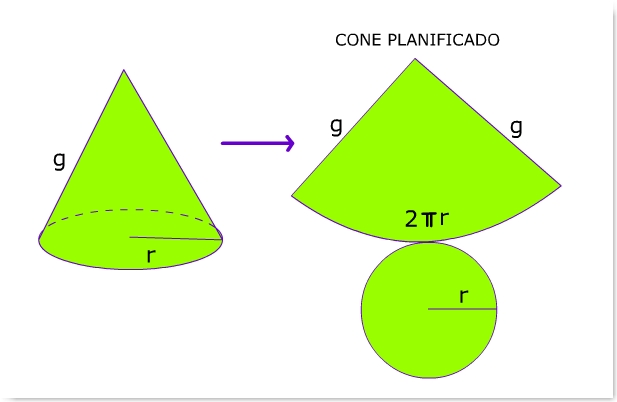
Fonte: imagem cedida pelo autor.
A área lateral (AL) de um cone é obtida por:
AL =
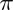. r. gA área da base (AB) é obtida por:
AB =
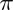. r2A área total (AT) é a soma da área da base e da área lateral. Portanto:
AT = AL + AB
Usando as expressões anteriores, obtemos:
AT =
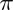. r (r + g)Volume
O volume do cone é dado pela expressão:
V = AT . h
3
Se AT =
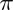. r2 Temos a fórmula para calcular o volume
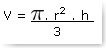fonte :Portal do professor (http://portaldoprofessor.mec.gov.br/)
Sem comentários:
Enviar um comentário